Dosimétrie des Rayonnements Ionisants

Dosimétrie des Rayonnements Ionisants

1. Introduction

1.1 Définition

La dosimétrie est un ensemble de méthodes et d’investigations (des mesures et des calculs) qui permet de déterminer et de spécifier de manière quantitative le dépôt d’énergie d’un rayonnement ionisant dans un point ou un volume d’intérêt par certains paramètres que l’on appelle grandeurs dosimétriques. Par ces derniers, on peut :

• Estimer le danger potentiel des techniques de diagnostic in vivo, en particulier d’imagerie utilisant des rayonnements ionisants.
• Optimiser les protocoles de traitement en radiothérapie en prévoyant l’énergie qui sera absorbée par les tissus tumoraux et les tissus sains.
• Établir les normes de radioprotection individuelles ou collectives.

1.2 Généralités sur les Rayonnements

Qu’est-ce qu’un rayonnement ? C’est un mode de transport spontané de l’énergie dans l’espace par une double vibration affectant un champ magnétique H H H et un champ électrique E E E, qui sont en phase et perpendiculaires entre eux. Ces champs s’engendrent mutuellement conformément aux lois de Maxwell. Ce déplacement dans le vide se fait à la vitesse de la lumière, définie par le vecteur K \mathbf{K} K.

• Intensité du champ électrique : exprimée en volts par mètre (V/m).
• Intensité du champ magnétique : exprimée en ampères par mètre (A/m).
• Impédance caractéristique du milieu : exprimée en ohms (Ω).

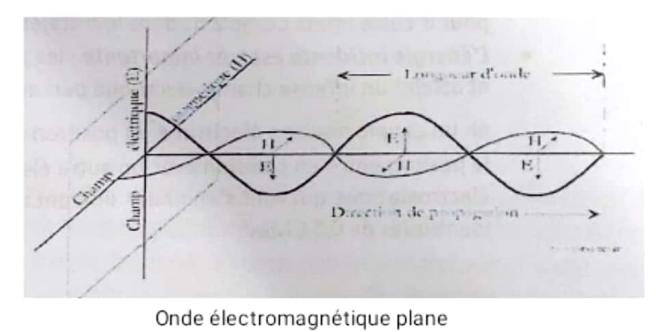
Une onde électromagnétique plane est dite ionisante lorsque l’énergie cédée par cette dernière est suffisante pour provoquer des ionisations (arracher un électron orbital). Cette énergie est donnée par un quantum E=hν E = h \nu E=hν (supérieure à l’énergie de liaison des électrons).

---

L’énergie d’un photon est donnée par la relation E=h⋅c/λ E = h \cdot c / \lambda E=h⋅c/λ. Après remplacement des constantes h h h (constante de Planck) et c c c (vitesse de la lumière) par leurs valeurs numériques, on obtient la formule de Duane et Hunt :
E=1240λE = \frac{1240}{\lambda} E=λ1240​
où E E E est en électronvolts (eV) et λ \lambda λ en nanomètres (nm).

Exemple :

• Pour créer une paire d’ions dans l’air, il faut déposer une énergie E=34 eV E = 34 \, \text{eV} E=34eV.
• Dans l’eau (tissus vivants), il faut E=32 eV E = 32 \, \text{eV} E=32eV.

Les Différents Types de Rayonnements

On peut classer les rayonnements ionisants selon :

1. Sa Nature Corpusculaire

• Photons : Grains d’énergie de masse et de charge nulles au repos, qui se matérialisent lorsqu’ils sont mis en mouvement à la vitesse c=3×108 m/s c = 3 \times 10^8 \, \text{m/s} c=3×108m/s. Exemples : rayonnements gamma et rayons X.
• Rayonnements particulaires : Particules de masse m m m au repos, qui peuvent être chargées ou non chargées :
  1. Particules chargées : Faisceaux d’électrons, de protons, et ions lourds.
  2. Particules non chargées : Faisceaux de neutrons rapides.

2. Sa Façon d’Ioniser la Matière

• Rayonnements indirectement ionisants : Photons X et gamma (via des électrons secondaires) et neutrons rapides (via des protons de recul).
• Rayonnements directement ionisants : Faisceaux de protons, d’électrons, et ions lourds.

3. Les Échanges Énergétiques entre le Rayonnement Ionisant et le Milieu Irradié

Le rayonnement ionisant (les photons) interagit avec la matière par son énergie véhiculée et entre en interaction avec ses constituants (électrons et noyau) :

• Énergie incidente faible : L’effet photoélectrique domine. L’énergie est cédée totalement à un électron périphérique faiblement lié, qui est mis en mouvement pour provoquer d’autres ionisations.
• Énergie incidente importante : L’effet Compton domine. L’énergie est cédée partiellement aux électrons périphériques pour d’autres ionisations, le reste étant émis sous forme de photons diffusés pour d’autres effets Compton.
• Énergie incidente très importante : Les photons deviennent plus pénétrants et atteignent un intense champ électrique périnucléaire, où ils se matérialisent en un couple neutre (électron et positron). L’électron retombe sur le noyau, tandis que le positron entre en collision avec un électron orbital, s’annihilant par force électrostatique et libérant deux photons d’énergies identiques de 0.51 MeV 0.51 \, \text{MeV} 0.51MeV.

---

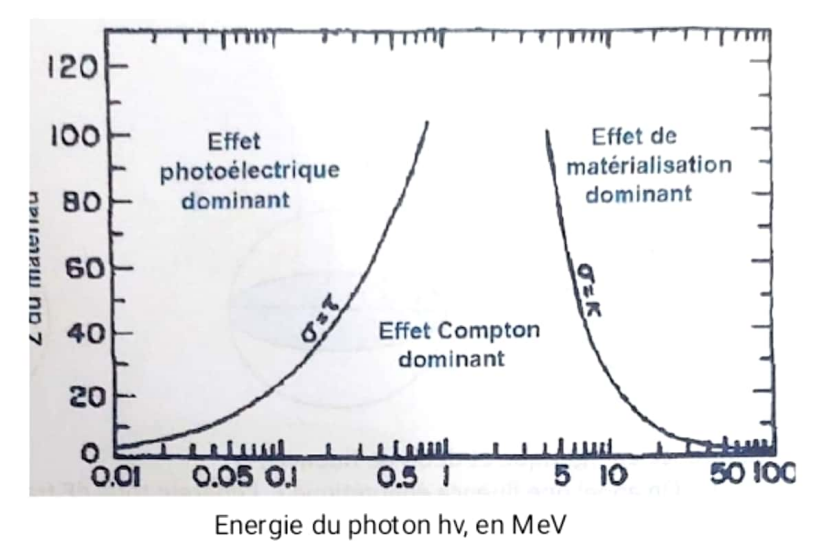
Figure II-4

Importance relative des trois principaux types d’interactions des rayons X et gamma. La courbe montre les valeurs de Z Z Z (numéro atomique) et E E E (énergie) pour lesquelles deux types d’effets sont égaux.

II. Les Grandeurs Dosimétriques

II.1 Le Flux et la Fluence

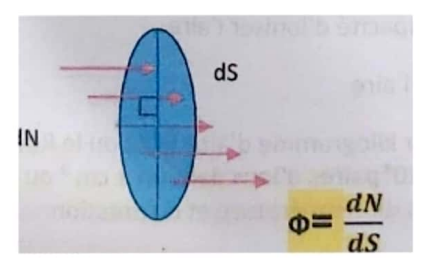
• Flux particulaire (Φ \Phi Φ) : Soit un faisceau de dN dN dN particules traversant une section surfacique dS dS dS dont les directions sont perpendiculaires au diamètre de la section. Le flux caractérise les rayonnements monodirectionnels.

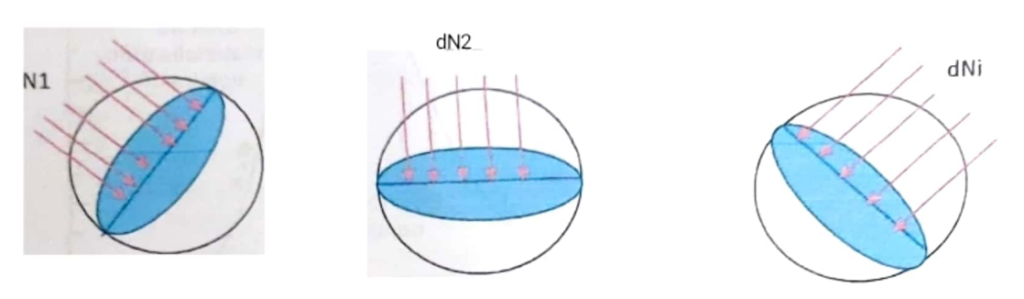
• Fluence particulaire (Ψ \Psi Ψ) : Soit dN dN dN le nombre de particules pénétrant dans une sphère de centre P P P et de section diamétrale dS dS dS, perpendiculaire à chaque direction des particules. La fluence est la somme des flux élémentaires traversant un volume sphérique centré sur le point P P P :
  Ψ=∑i=1ndNdS\Psi = \sum_{i=1}^n \frac{dN}{dS} Ψ=∑i=1n​dSdN​
  La fluence caractérise les rayonnements multidirectionnels.

---

La Fluence Énergétique et le Débit de Fluence

1. Fluence énergétique (F F F) : Énergie totale dE dE dE transportée par les particules, divisée par la surface de la section diamétrale de la sphère élémentaire :
   F=dEdSF = \frac{dE}{dS} F=dSdE​
2. Débit de fluence (Ψ˙ \dot{\Psi} Ψ˙) : Variation de la fluence par unité de temps, pour caractériser l’instant t t t :
   Ψ˙=dΨdt\dot{\Psi} = \frac{d\Psi}{dt} Ψ˙=dtdΨ​

II.2 L’Exposition

L’exposition X X X est le quotient de la charge dQ dQ dQ par élément de masse dm dm dm, où dQ dQ dQ est la valeur absolue de la charge totale des ions de même signe dans l’air :
X=dQdmX = \frac{dQ}{dm} X=dmdQ​

• Elle caractérise la capacité d’ioniser l’air.
• Elle ne concerne que l’air.
• Unité : joule par kilogramme (J/kg \text{J/kg} J/kg) ou Roentgen (R \text{R} R), où 1 R=2.58×10−4 J/kg 1 \, \text{R} = 2.58 \times 10^{-4} \, \text{J/kg} 1R=2.58×10−4J/kg.
  • 1 R 1 \, \text{R} 1R correspond à la création de 2.08×109 2.08 \times 10^9 2.08×109 paires d’ions dans 1 cm3 1 \, \text{cm}^3 1cm3 (ou 0.0013 g 0.0013 \, \text{g} 0.0013g d’air sec) dans des conditions normales de température et de pression.

II.3 La Loi des Inverses Carrés des Distances

L’atténuation d’un faisceau de photons dans l’air est très faible. Soit N N N le nombre de particules du faisceau incident traversant deux surfaces S1 S_1 S1​ et S2 S_2 S2​, situées à des distances L1 L_1 L1​ et L2 L_2 L2​, avec des fluences Φ1 \Phi_1 Φ1​ et Φ2 \Phi_2 Φ2​ respectivement :
Φ1=NS1,Φ2=NS2,Φ1Φ2=S1S2\Phi_1 = \frac{N}{S_1}, \quad \Phi_2 = \frac{N}{S_2}, \quad \frac{\Phi_1}{\Phi_2} = \frac{S_1}{S_2} Φ1​=S1​N​,Φ2​=S2​N​,Φ2​Φ1​​=S2​S1​​

---

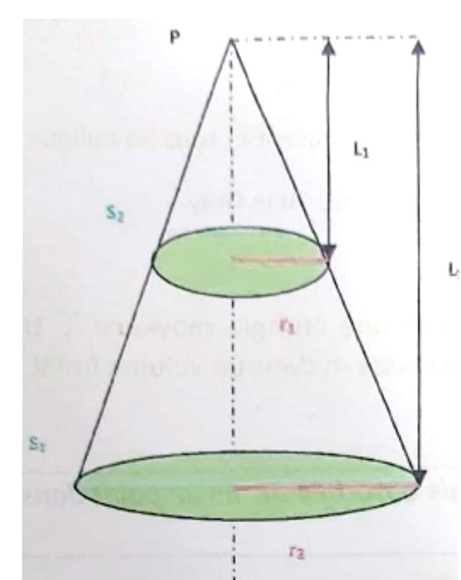
S1=π⋅r12,S2=π⋅r22,r1L1=r2L2 S_1 = \pi \cdot r_1^2, \quad S_2 = \pi \cdot r_2^2, \quad \frac{r_1}{L_1} = \frac{r_2}{L_2} S1​=π⋅r12​,S2​=π⋅r22​,L1​r1​​=L2​r2​​ (selon la loi de Thalès).
Pour les doses absorbées D1 D_1 D1​ et D2 D_2 D2​ aux distances L1 L_1 L1​ et L2 L_2 L2​ :
D1D2=(L2L1)2\frac{D_1}{D_2} = \left( \frac{L_2}{L_1} \right)^2 D2​D1​​=(L1​L2​​)2
D1=D2×(L2L1)2D_1 = D_2 \times \left( \frac{L_2}{L_1} \right)^2 D1​=D2​×(L1​L2​​)2
Ainsi, la dose absorbée en un point dans l’air varie comme l’inverse du carré de sa distance à la source.

II.4 Le KERMA

Le KERMA (K K K, Kinetic Energy Released in Material) est défini comme l’énergie moyenne transférée dEtr dE_{tr} dEtr​ d’une radiation indirectement ionisante aux particules chargées (électrons) dans le milieu, par unité de masse dm dm dm :
K=dEtrdmK = \frac{dE_{tr}}{dm} K=dmdEtr​​

• Unité : joule par kilogramme (J/kg \text{J/kg} J/kg) ou Gray (Gy \text{Gy} Gy).
• Concerne uniquement les rayonnements indirectement ionisants.
• Applicable à tous les milieux.

II.5 Le CEMA

Le CEMA (Converted Energy per unit Mass) est une quantité non stochastique applicable aux radiations directement ionisantes (électrons, protons). Le CEMA C C C est le quotient de dEc dE_c dEc​ par dm dm dm, où dEc dE_c dEc​ est l’énergie perdue par les particules chargées (sauf les électrons secondaires) dans des collisions par unité de masse dm dm dm :
C=dEcdmC = \frac{dE_c}{dm} C=dmdEc​​

---

• Concerne uniquement les rayonnements directement ionisants.
• Applicable à tous les milieux irradiés.
• Unité : joule par kilogramme (J/kg \text{J/kg} J/kg) ou Gray (Gy \text{Gy} Gy).

II.6 La Dose Absorbée

La dose absorbée D D D est définie comme l’énergie moyenne dEabs dE_{abs} dEabs​ transmise par une particule ionisante à la matière d’une masse dm dm dm dans un volume fini V V V :
D=dEabsdmD = \frac{dE_{abs}}{dm} D=dmdEabs​​

• Concerne tous les rayonnements et tous les milieux.
• Unité : joule par kilogramme (J/kg \text{J/kg} J/kg) ou Gray (Gy \text{Gy} Gy).

III. Les Paramètres Temporels

1. Débit de dose (D˙ \dot{D} D˙) : Accroissement de la dose par unité de temps.
   • Unité : Gray par seconde (Gy/s \text{Gy/s} Gy/s) ou Gray par heure (Gy/h \text{Gy/h} Gy/h).
2. Débit de KERMA (K˙ \dot{K} K˙) : Variation du KERMA dK dK dK par rapport au temps dt dt dt :
   K˙=dKdt\dot{K} = \frac{dK}{dt} K˙=dtdK​
   • Unité : Gray par seconde (Gy/s \text{Gy/s} Gy/s) ou Gray par heure (Gy/h \text{Gy/h} Gy/h).
3. Débit de l’exposition (X˙ \dot{X} X˙) : Variation de l’exposition dX dX dX par rapport au temps dt dt dt :
   X˙=dXdt\dot{X} = \frac{dX}{dt} X˙=dtdX​
   • Unité : Roentgen par seconde (R/s \text{R/s} R/s) ou Roentgen par heure (R/h \text{R/h} R/h).

Dosimétrie des Rayonnements Ionisants

Voici une sélection de livres:

Parodontologie Relié – 1 novembre 2005

Guide pratique de chirurgie parodontale Broché – 19 octobre 2011

Parodontologie Broché – 19 septembre 1996

MEDECINE ORALE ET CHIRURGIE ORALE PARODONTOLOGIE

Parodontologie: Le contrôle du facteur bactérien par le practicien et par le patient

Parodontologie clinique: Dentisterie implantaire, traitements et santé

Parodontologie & Dentisterie implantaire : Volume 1

Endodontie, prothese et parodontologie

La parodontologie tout simplement Broché – Grand livre, 1 juillet 2020

Dosimétrie des Rayonnements Ionisants